[컴퓨터구조] ch.4 레지스터 전송과 마이크로 연산 (2) 마이크로 연산

Mano의 컴퓨터시스템구조 제3판, 프로텍 미디어, 김종상 옮김 도서를 정리, 요약하는 글입니다.

 

1. 기본적인 마이크로 연산

- 레지스터 사이에서 이진 정보 전송

- 레지스터에 저장된 수치 데이터에 대해서 산술 연산 수행

- 레지스터에 저장된 비수치 데이터에 대해 비트 조작 연산 수행

- 레지스터에 저장된 데이터에 대해 시프트 연산 수행

 

2. 산술 마이크로 연산

사진 출처 : https://upscfever.com/upsc-fever/en/gatecse/en-gatecse-chp152.html

 

- 기본적인 산술 마이크로 연산에는 위 그림과 같이 덧셈, 뺄셈, 인크리멘트, 디크리멘트, 시프드 등이 있다.

- 곱셈과 나눗셈은 산술 연산이지만 위 그림의 기본 연산 집합에 포함되지 않는다. 곱셈과 나눗셈은 디지털 시스템에서 조합 회로로 구현했을 때에 마이크로 연산으로 간주한다.

 

(1) 이진 가산기

- 전 가산기(full adder) : 2 비트와 이전 캐리의 산술 합 계산하는 디지털 회로

- 이진 가산기(binary adder) : 임의의 길이를 가진 두 이진수에 대한 덧셈 수행하는 회로

 

사진 출처 : https://upscfever.com/upsc-fever/en/gatecse/en-gatecse-chp152.html

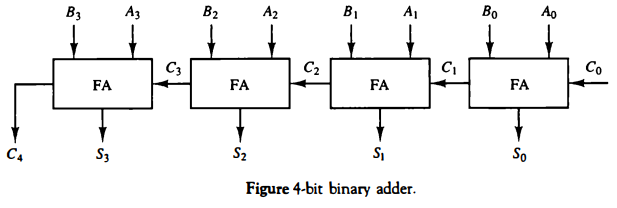
- 일반적으로 n비트의 이진 가산기는 n개의 전가산기로 이루어진다. 각 전가산기의 캐리 출력은 다음 상위 전가산기의 캐리 입력에 연결된다. 

 

(2) 이진 가감산기

- 이진수의 뺄셈은 1의 보수 덧셈으로 계산한다. 이진 가감산기는 각 전가산기에 exclusive OR 게이트를 추가하여 구현한다.

- 모드(mode) 입력 M이 0이면 가산기, 1이면 감산기로 동작한다.

사진 출처 : https://suyeon96.tistory.com/7

 

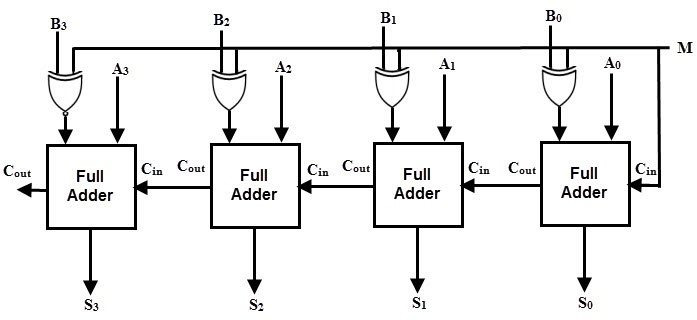
- M = 0일 때, B ⊕ 0 = B가 되어 전가산기에는 B가 입력되고, 입력 게이트 Cin에는 0이 들어가 결국 B + 0인 덧셈이 된다.

- M = 1일 때, B ⊕ 1 = B'가 되어 전가산기 입력에는 B'가 입력되고 Cin에는 1이 들어가므로 B' + 1이 된다. 이것은 2의 보수 덧셈 즉 뺄셈이 된다. 부호가 없는 숫자의 경우 A >= B이면 A - B가 출력되고 A < B이면 B - A에 대한 2의 보수가 출력으로 나온다.

 

(3) 이진 인크리멘트

사진 출처 : https://upscfever.com/upsc-fever/en/gatecse/en-gatecse-chp152.html

 

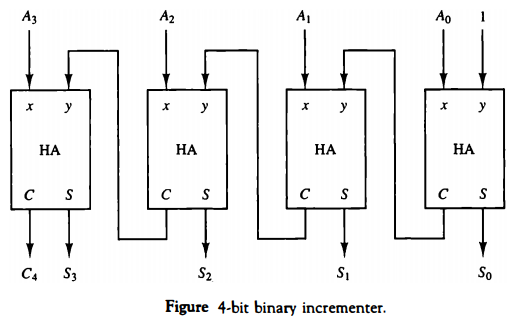
- 인크리멘트 마이크로 연산은 레지스터 값에 1을 더하는 것이다. 예르 들어 A가 0011이라면 인크리멘트(+1) 한 이후에는 0100이 되어야 한다. 

- 카운트 enable이 활성화될 때 클럭 펄스의 변이에 의해 레지스터 값이 하나씩 증가하게 된다. 하지만 인크리멘트 연산은 특정한 레지스터와 관계없이 조합 회로에 의해서 수행되어야 하는 경우가 있다. 그럴 경우 반가산기(half adder : HA)를 직렬로 연결하여 위 그림과 같이 구현한다.

 

(4) 산술 회로

사진 출처 : https://upscfever.com/upsc-fever/en/gatecse/en-gatecse-chp152.html

 

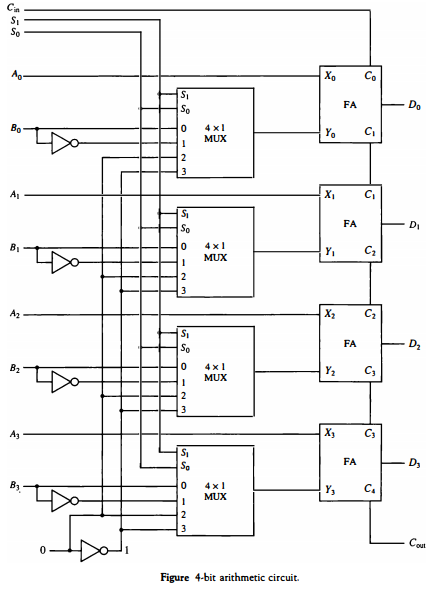
- 이렇게 4비트 산술 회로를 구성하면 가산기(FA)에 들어갈 데이터 입력을 제어하여 다양한 연산이 가능하다. 위 그림으로는 서로 다른 7가지 연산이 가능하다. 

 

- 현재 이 회로에서 이진 가산기(FA)의 출력은 D = A + Y + Cin이다.

- s1s0 = 00이면 각 멀티플렉서의 0번인 B가 선택(B0, B1, B2, B3 선택) 되어 Y 입력이 된다. 가산기의 입력으로 A가 들어가며 결국 D = A + B + Cin이다. Cin = 0 이면 A + B 이고, Cin = 1이면 A + B + 1이다. 

- s1s0 = 01이면 각 멀티플렉서의 1번인 B'가 선택되어 Y 입력이 된다. Cin이 1이면 D = A + B' + 1 이므로 A + B의 2의 보수이다. Cin이 0이면 D = A + B'이므로 A - B - 1이 된다.

- s1s0 = 10이면 B는 무시되고 가산기에 0이 입력된다. Cin이 1이면 D = A + 0 + 1 즉 A + 1이고, Cin이 0이면 D = A이다.

- s1s0 = 11이면 가산기에 1이 입력되므로 Cin이 0이면 D = A - 1과 같은 디크리멘트 연산을 수행한다. Cin이 1이면 D = A - 1 + 1이므로 A가 그냥 출력되는 것과 같다. 모든 연산을 정리한 것은 아래 그림과 같다.

 

사진 출처 : https://upscfever.com/upsc-fever/en/gatecse/en-gatecse-chp152.html