1. 점근적 분석의 필요성
- 알고리즘 설계에는 다양한 방법이 있다. 알고리즘이 얼마나 효율적인지 성능을 분석해야 할 때 점근적 분석이 필요하다.
- 물론 크기가 작은 문제는 알고리즘의 효율이 크게 중요하지 않다. 비효율적인 알고리즘도 무방하다고 할 수 있다. 하지만 크기가 충분히 큰 문제에서는 알고리즘 분석은 매우 중요하다. 즉 입력의 크기가 충분히 큰 경우에 대한 분석을 점근적 분석이라 한다.
- 알고리즘의 실행 시간, 필요한 메모리 크기, 통신 등등 자원이 얼마나 소모되는 지 분석한다.
2. 점근적 분석의 특징
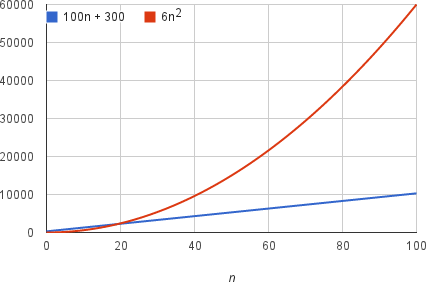
- 점근적 분석은 입력의 크기에 따라 이 알고리즘의 실행시간이 얼마나 걸리는 지 분석한다. 입력 크기에 따른 실행시간을 나타낸 함수를 성장률이라고 한다.
- 위의 그래프처럼 100n + 300과 6n2의 성장률을 볼 때, n2의 성장률이 기하급수적으로 커진다. 즉 입력이 커질 수록 n2의 실행 시간이 기하급수적으로 느려짐을 알 수 있다.
- 여기서 가장 높은 차수의 항만 계산하고 계수, 상수는 특별히 생각하지 않는다 .성장률에 크게 영향을 미치지 않기 때문이다.
3. 점근적 표기법 (1) 빅오(big O) 표기법
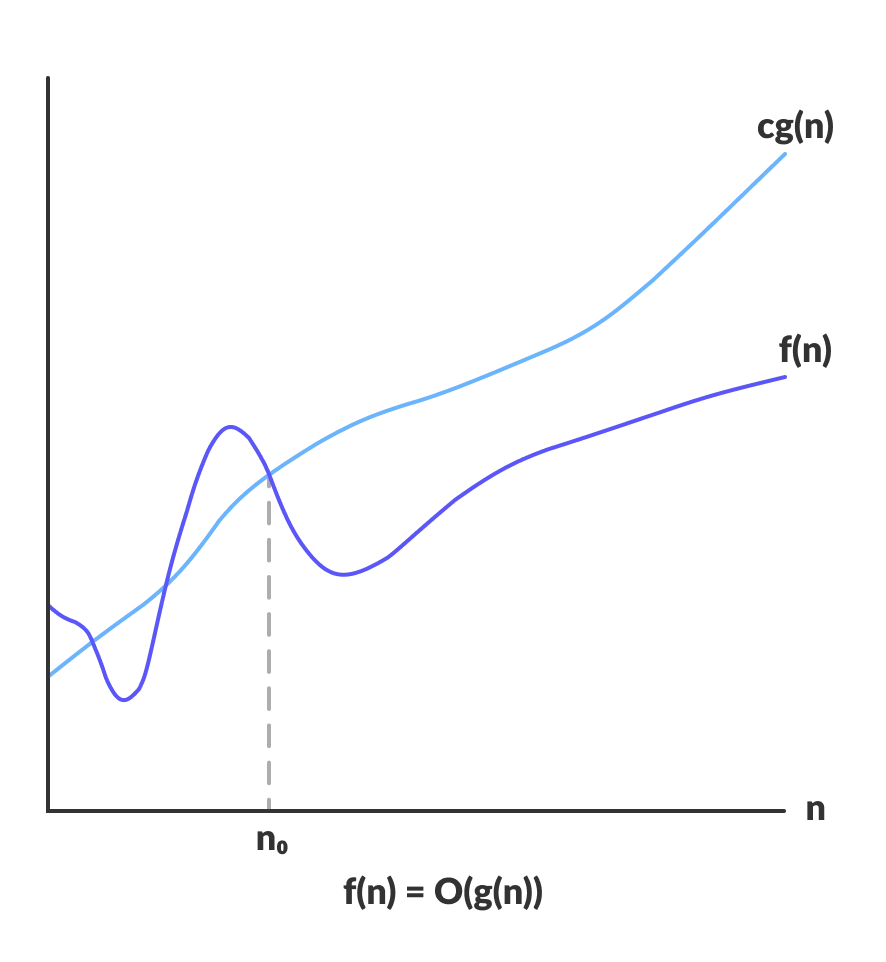
- 빅오(big O) formal definition : O(g(n)) = { f(n) | ∃c > 0, n0 ≥ 0 s.t.∀n ≥ n0, cg(n) ≥ f(n) }
- 모든 n, n0에 대해서 f(n) <= cg(n)인 조건을 만족시키는 두 양의 상수 c와 n0가 존재한다면 f(n) ∈ O(g(n))이다. 이를 관행적으로 f(n) = O(g(n))이라고 쓴다.
- 점근적 상한(upper bound)만 알고 있을 때 빅오 표기법을 쓴다. 실행 시간이 이 상한을 넘지는 않는 것이다. 다시 말해 알고리즘이 최악의 경우에도 이 기준은 넘지 않는다라고 할 수 있다.
- 그래프를 보면 어떤 기준점부터는 f(n)은 cg(n)보다 증가율이 같거나 느리다. 즉 f(n) 알고리즘이 cg(n)보다 더 빨리 실행된다. 아무리 나빠도 f(n)은 cg(n)보다 같거나 낫다.
- 상한의 개념은 중요하다. 언제나 최악의 경우를 생각해야 하기 때문에 빅오 표기법이 많이 쓰인다.
4. 점근적 표기법 (2) 오메가(Ω) 표기법

- 빅 오메가(big omega) formal definition : Ω(g(n)) = { f(n) | ∃c > 0, n0 ≥ 0 s.t.∀n ≥ n0, cg(n) ≤ f(n) }
- 모든 n, n0에 대해서 f(n) >= cg(n)인 조건을 만족시키는 두 양의 상수 c와 n0가 존재한다면 f(n) ∈ Ω(g(n))이다. 이를 관행적으로 f(n) = Ω(g(n))이라고 쓴다.
- 점근적 하한(lower bound)만 알고 있을 때 오메가 표기법을 쓴다. 적어도 g(n)의 비율로 증가하는 함수이기 때문에 O(g(n))과는 대칭적이다. (상한이 없이) 하한을 기준으로 최소한 어느정도 걸린다고 할 때 쓸 수 있다.
- 그래프를 보면 f(n)의 증가율은 cg(n)보다 같거나 빠르다. 즉 f(n) 알고리즘이 더 느리게 수행된다. 결국 아무리 빨라도 이 기준보다 더 빠를 순 없다고 할 수 있다.
- 오메가 표기법은 사실상 큰 의미가 없다. 최선의 경우를 생각하는 것이 별 의미가 없기 때문.
5. 점근적 표기법(3) 세타(θ) 표기법

- 빅 세타(big theta) formal definition : θ(g(n)) = O(g(n)) ∩ Ω(g(n))
- 모든 n, n >= n0에 대해 c1g(n) <= f(n) <= c2g(n)을 만족하면 f(n) = θ(g(n))이다.
- 상한과 하한을 모두 알고 있을 때, 세타 표기법을 쓴다. f(n)은 상한과 하한의 중간 평균 어디쯤이라고 할 수 있다.
- 그래프 상으로 결국 f(n)은 g(n)의 비율로 증가하는 함수라고 할 수 있다.
6. 빅오 표기법 예시 그래프
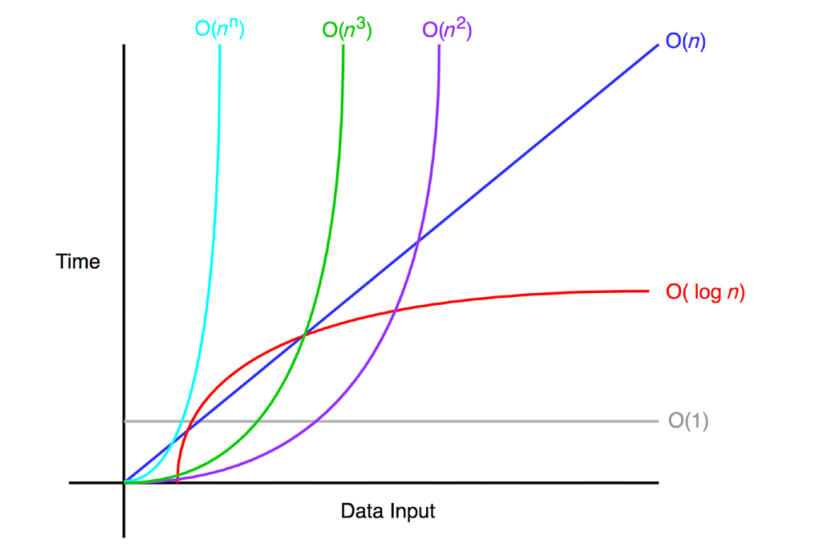
- O(1) : 상수형 (사칙연산, if문, 해시 테이블)
- O(logn) : 로그형 (이진탐색)
- O(n) : 선형 (순차탐색)
- O(nlogn) : 선형로그형 (분할 정복 알고리즘)
- O(n2) : 평방형 (2중 for문)